Introduction
It’s been a long time since I updated this blog! I’m hoping to be able to update it at least a few more times this year, as I have some ideas for posts which I think some people may find useful. One post will (finally!) cover how to use TPUs with GALLOP. It’s taken this long because the free TPU resources available online up to this point have been extremely limited. Fortunately, Kaggle have given their users a generous TPU quota and importantly, access to a powerful enough VM to make the most of the performance of the TPU using pytorch, which is the library GALLOP uses for all of its calculations. I am also working on some stuff unrelated to GALLOP which I’m quite excited about, with a focus on PXRD indexing. I’m hoping to get it written up as a paper before the end of the year. If I manage that (and it’s a big if), there will be an accompanying blog post giving an informal summary of the work.
This post
This is a very brief follow up to a previous post in which we looked at using GALLOP to optimise using the profile rather than intensity \(\chi^2\) figure of merit. In that post, we showed that doing this potentially provides a small level of benefit in terms of the speed with which the runs are completed, though the number of solutions and frequency with which they are obtained is not significantly affected. As the bulk of the time spent by GALLOP is used for conversion of internal coordinates to Cartesian coordinates, the potential performance benefits are somewhat limited. Despite this, I’ve added the functionality to the latest version of GALLOP so you can try it for yourself. At the moment, this functionality is limited to data that has been fitted using DASH.
In this post, I want to talk about an idea I had recently on a situation in which this added capability in GALLOP may be useful.
Pawley refinement in DASH
The user interface for preparing a dataset for crystal structure determination in DASH is very user friendly and intuitive. The wizard guides the user through trimming the data, background subtraction, indexing, space group determination and finally intensity extraction. However, despite the user friendly wizard, the Pawley refinement process is not without its quirks.
Quite often, if you have not trimmed the data down to a low enough resolution, you will run across the following error message:
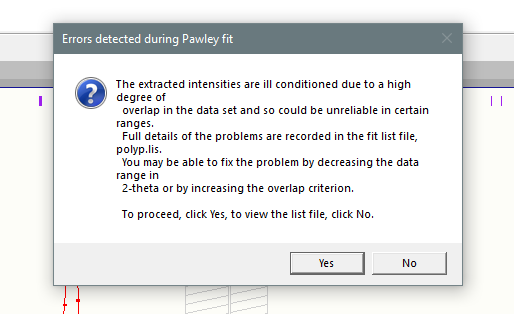
As you can see, the recommended course of action is to either trim the data to a lower resolution or increase the overlap criterion. This might be despite what looks like a good fit to the data:
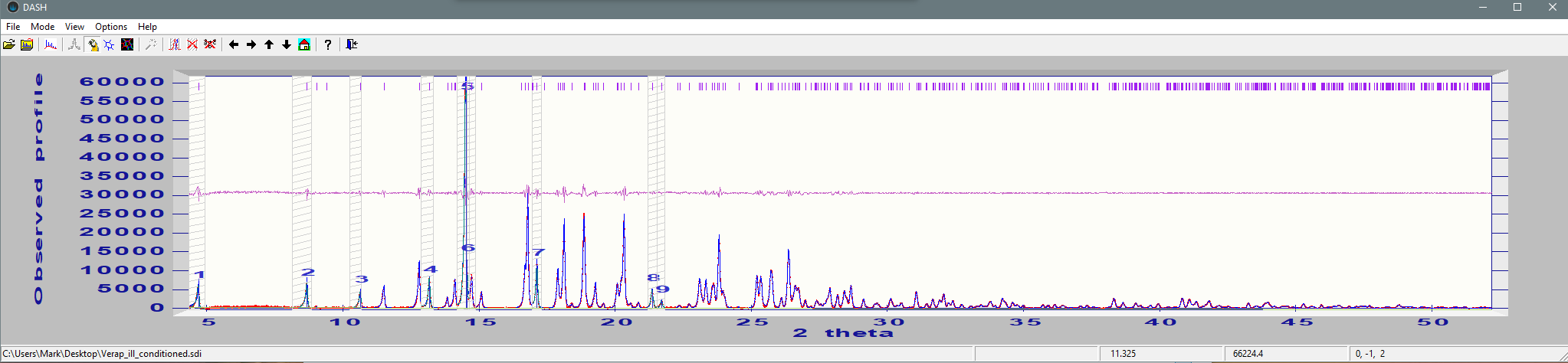
The question then is, can we still solve the crystal structure despite this issue?
Solving despite an ill conditioned Pawley covariance matrix
I used verapamil hydrochloride (yet again!) as the test case for this particular idea. The example data supplied with GALLOP has been fitted with DASH to about 2.24 Å (equivalent to 40.2° \(2\theta\) with Cu \(K_{\alpha_{1}}\) radiation). I chose to refit the data, this time out to 1.75 Å (which is equivalent to 52.2° \(2\theta\) with Cu \(K_{\alpha_{1}}\)) using DASH.
Unsurprisingly, given the much better resolution, there is a significant increase in the number of reflections for which intensities are extracted: 252 in the lower resolution data, 531 in the higher resolution data. As a result, the DASH Pawley routine gives the ill conditioning error message seen in the previous section. Despite the error, I chose to “accept” the result of the refinement during each iteration, saving the Pawley files and proceeding with GALLOP as normal.
Using GALLOP, I attempted to solve the crystal structure using 20 swarms of 1000 particles both with the intensity \(\chi^2\) and profile \(\chi^2\) figures of merit. On the supplied example data in GALLOP, this number of swarms and particles is usually sufficient to solve the structure multiple times within 10 iterations, and generally gives a very low RMSD to the published crystal structure.
Results
Despite running for over 15 iterations, no solutions were obtained using the intensity \(\chi^2\) figure of merit. However, using the profile \(\chi^2\), I was able to obtain a solution in 4 GALLOP iterations, which is in line with performance obtained with data that does not suffer from ill conditioning. The RMSD obtained with Mercury is also excellent - just 0.098 Å!
Conclusions
If we are using DASH to do our Pawley refinements, sometimes we are forced to reduce the resolution of the data we are working with or modify other parameters such as the peak overlap criterion in an effort to avoid ill conditioning of the Pawley covariance matrix. Ill conditioning prevents the intensity \(\chi^2\) figure of merit from providing an accurate assessment of the agreement between the observed and calculated intensities, and hence in DASH this provides an impediment to solving the crystal structure.
In this blog post, we’ve seen that even when this occurs, it is still possible to solve the crystal structure using the profile \(\chi^2\) figure of merit, which is not affected by the covariance matrix obtained during the Pawley refinement.
As such, if you are limited to using DASH for intensity extraction and a dataset is proving difficult to manage, it may be possible to solve the structure despite ill conditioning. However, in addition to the strategy presented in this post, I would also recommend trying alternative refinement software such as GSAS-II, which may work more reliably on the dataset you are using than DASH.